A aula anterior tratou do sistema de capitalização simples e esta aula será sobre o sistema de capitalização composta, também conhecida como “juros compostos”. Nesse sistema, a base sobre a qual incidirão os juros é composta pelo principal mais os juros recebidos anteriormente.
O valor futuro considerando apenas o primeiro período é o mesmo tanto na capitalização simples quanto na composta:
VF = VP + VP × i = VP × ( 1 + i )
O valor futuro do segundo período é o valor do primeiro mais os juros do segundo, que incluem na sua base de cálculo o valor futuro do primeiro período:
VF = VP + VP × i + ( VP + VP × i ) × i = VP + 2.VP.i + i² = VP.( 1 + i )²
Para n períodos, o valor futuro é:
VF = VP.( 1 + i )n
Onde:
n = Número de Períodos
i = Taxa de juros
Exemplo:
Um investidor realizou uma aplicação financeira de R$ 1.000,00 com prazo de 5 anos e taxa de 10% a.a.
Notícias Relacionadas
Presidente do banco também negou boatos sobre JBS
CEO do Bradesco nega que Ágora tenha suspendido CDBs do Master; diz que ´pode ter maldade´ em rumor
Por: Luciano Costa São Paulo, 31/10/2024 – O presidente do Bradesco, Marcelo Noronha, negou hoje que a corretora Ágora, controlada pelo banco, tenha suspendido a oferta de CDBs do Banco Master a clientes, informação que circulou no mercado nos últimos dias. “Sendo franco com você, isso da Ágora não existe”, disse o CEO, ao ser […]
Leilão Tesouro Nacional
Leilões de títulos do Tesouro têm taxas recordes em meio à desconfiança com fiscal
São Paulo, 17/10/2024 – Em meio à crise de confiança do mercado em relação à condução do ajuste fiscal prometido pelo governo do presidente Luiz Inácio Lula da Silva (PT), operadores têm exigido altos prêmios pelos títulos ofertados pelo Tesouro Nacional em leilões nesta semana, que registraram as maiores taxas do ano. De acordo com o […]
VF = 1000.(1+10%)5 = 1.610,51
Rearranjando os termos da fórmula de valor futuro, é possível chegar às demais variáveis. Para o valor presente:
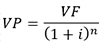
Para a taxa de juros:
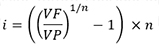
O número de períodos com juros compostos é mais complicado e exige mais do que as quatro operações básicas:
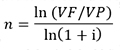
Onde:
ln é o logaritmo natural.
No Excel, basta usar a fórmula ln
Usando o exemplo anterior:
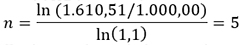
O cálculo do prazo pode ser utilizado para determinar quanto tempo irá demorar para multiplicar o capital por um certo valor, trocando VF/VP pelo multiplicador. Por exemplo, quantos meses seriam necessários para dobrar o capital aplicando à taxa de 0,5% ao mês.
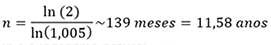
Assim como ocorre com juros simples, é necessário trabalhar com as variáveis na mesma periodicidade, ou seja, se o período é em anos, a taxa deve ser anual. Para converter uma taxa anual em mensal:
Taxa mensal = (1 + Taxa Anual)1/12O regime de capitalização composta é o mais utilizado, tanto para aplicações financeiras, quanto para empréstimos, de forma que as aulas posteriores irão considerar apenas cálculos com juros compostos.
Até aqui, foram ensinados os principais cálculos de Matemática Financeira em situações simples onde há apenas um valor presente e um valor futuro. Nas próximas aulas, essas técnicas serão aplicadas para séries de fluxos de caixa.
