Neste texto, iremos falar sobre mais uma medida de risco de títulos de renda fixa, a convexidade. Essa medida é um refinamento das medidas de duration que abordamos em textos anteriores. Para facilitar o entendimento, o texto está dividido nos seguintes tópicos:
- A Convexidade dos Preços dos Títulos e o Yield
- Conhecendo a fórmula da Convexidade
- Exemplo prático: Duration vs. Convexidade
- Referências
Boa leitura!
A Convexidade dos Preços dos Títulos e o Yield
A medida de duração indica que, independentemente das taxas de juros aumentarem ou diminuírem, a variação percentual aproximada do preço é a mesma. No entanto, temos que admitir que isso nem sempre é tão exato como calculado com a duration e suas variantes.
Primeiramente, vamos explicar essa confusão. Em um primeiro momento, a duração pode ser uma boa medida de como os preços dos títulos podem ser afetados devido a pequenas e repentinas flutuações nas taxas de juros (o que chamamos de yield). No entanto, a relação entre os preços dos títulos e o yield não é linear de fato.
Portanto, a convexidade é uma medida melhor para avaliar o impacto nos preços dos títulos quando existem grandes flutuações nas taxas de juros.
Exemplo gráfico
Abaixo, temos uma apresentação gráfica da convexidade de dois títulos A e B. Você pode ver que, caso tivéssemos calculado a duration, teríamos obtido a linha azul. Ou seja, uma estimativa da mudança linear do preço do título, dada uma mudança na taxa de juros.
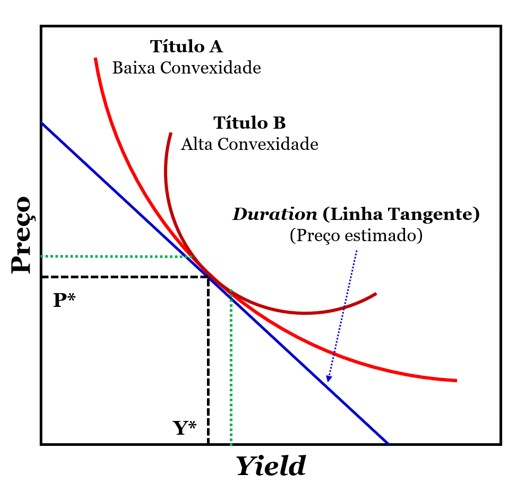
Fonte: adaptado de Fabozzi (2012)
Ambos os títulos A e B teriam a mesma duration e poderíamos dizer que ambos iriam variar igualmente com as mudanças no yield. Entretanto, isso não é verdade! De fato, em pequenas mudanças, é praticamente impossível notar que os dois títulos são diferentes (veja a linha tracejada em verde, o preço dos títulos A e B e a estimativa da duration é praticamente a mesma). Porém, para mudanças maiores, podemos ver que a variação no preço do Título B é muito maior!
Abaixo, temos a variação no preço de um título com preço atual de V0 = 113.6777, que paga cupons de 5%, maturidade de 20 anos e yield de 4%. Nota-se que a duration consegue captar a mudança no preço em pequenas mudanças no yield. Porém, quando temos mudanças súbitas, a mudança no preço estimada com a duration se afasta do preço real calculado com uso da fórmula da avaliação de títulos.
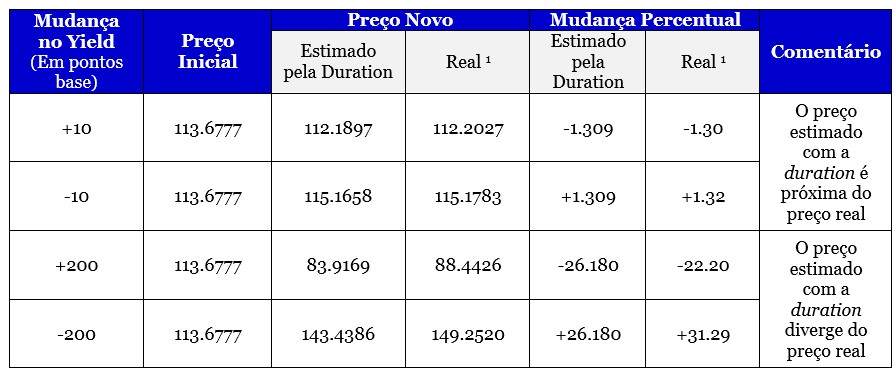
Nota: calculado usando a fórmula padrão de avaliação de bond
A razão para esse resultado é que a duration é, de fato, uma primeira aproximação (linear) para uma pequena mudança no yield. A aproximação pode ser melhorada usando uma segunda aproximação. Essa aproximação é a convexidade. Assim, a medida de convexidade de um título pode ser usada para aproximar a mudança de preço que não é explicada pela duração.
Conhecendo a fórmula da Convexidade
A medida de convexidade de uma ligação é aproximada usando a seguinte fórmula:
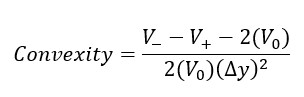
Essa fórmula é similar à fórmula conceitual da duration. Acontece que as variações da duration são aproximações para tornar o cálculo mais rápido e ter uma métrica das oscilações preço-yield. Aqui, temos uma fórmula mais exata.
Exemplo prático: Duration vs. Convexidade
Imagine um título com cupom de 5% (semestral), maturidade de 20 anos e yield de 4% e cujo preço atual é de V0 = 113.6777. O valor de face é de 100. Nesse sentido, vamos alterar o rendimento para cima e para baixo em 20 pontos base e determinar quais serão os novos preços para o numerador. Se o rendimento diminuir em 20 pontos base de 4,0% para 3,8%, o preço aumentará para 116,7049. Se o rendimento aumentar em 20 pontos base, o preço diminuiria para 110,7527.
Estes valores são obtidos com a fórmula abaixo.

Observação: usando a mesma fórmula, mas variando a taxa de juros para 4,2% e 3,8%, temos os valores 110,7527 e 116,7049, respectivamente.
Agora, vamos simular a variação de 0.002 no yield usando a fórmula da convexidade. Neste caso, temos:
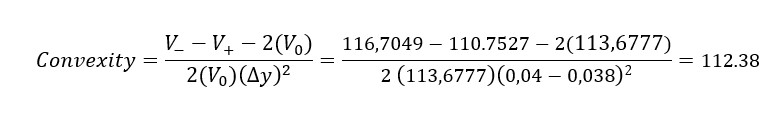
Adiantamos que não existe uma interpretação simples para o número obtido acima.
Dada a medida de convexidade, o ajuste aproximado da variação percentual do preço devido à convexidade do título (ou seja, a variação percentual do preço não explicada pela duração) é obtida pela fórmula abaixo.
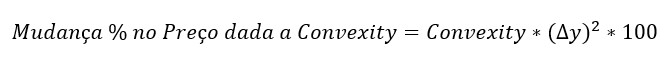
Duration vs. Convexidade
Usando com os dados do exemplo, vamos simular uma mudança de +2% no valor do título. Ou seja, de 4% para 6% (essa é uma mudança brusca! Imagine o tempo que levou para cair 200 pontos base a Selic). Se usássemos a duration, teriam uma variação estimada de -26.18% e um novo preço estimado em 83.9169.
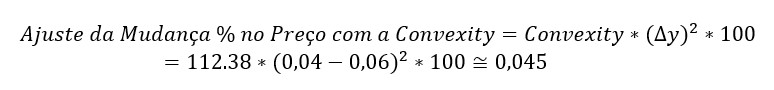
Calma, isso não quer dizer que o preço vai mudar apenas 4,5%. Em seguida, temos que somar estes 4,5% com a duration do título para fazer o ajuste da curvatura!

Agora, temos a mudança no preço ajustava a convexidade do título:
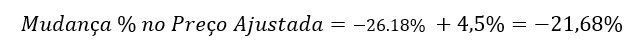
Logo, com estes novos valores, temos uma aproximação da real mudança no preço do título para mudanças bruscas nas taxas de juros, cujo cálculo exato é de -22.20% (Veja a Tabela acima)
Referências
FABOZZI, F. (2012). THE HANDBOOK OF FIXED INCOME SECURITIES. 8. Ed. McGraw-Hill.